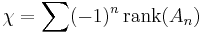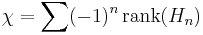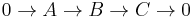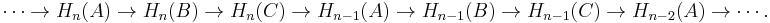Homology (mathematics)
In mathematics (especially algebraic topology and abstract algebra), homology (in part from Greek ὁμόιος homos "identical") is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group. See homology theory for more background, or singular homology for a concrete version for topological spaces, or group cohomology for a concrete version for groups.
For a topological space, the homology groups are generally much easier to compute than the homotopy groups, and consequently one usually will have an easier time working with homology to aid in the classification of spaces.
The original motivation for defining homology groups is the commonplace observation that one aspect of the shape of an object is its holes. But because a hole is "not there", it is not immediately obvious how to define a hole, or how to distinguish between different kinds of holes. Homology is a rigorous mathematical method for detecting and categorizing holes in a shape. As it turns out, there exist subtle kinds of holes that homology cannot "see" — in which case homotopy groups may be what is needed.
Contents |
Construction of homology groups
The construction begins with an object such as a topological space  , on which one first defines a chain complex
, on which one first defines a chain complex 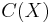 encoding information about
encoding information about  . A chain complex is a sequence of abelian groups or modules
. A chain complex is a sequence of abelian groups or modules 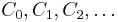 connected by homomorphisms
connected by homomorphisms 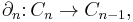 which are called boundary operators. That is,
which are called boundary operators. That is,
where 0 denotes the trivial group and 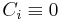 for
for 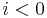 . It is also required that the composition of any two consecutive boundary operators be trivial. That is, for all
. It is also required that the composition of any two consecutive boundary operators be trivial. That is, for all  ,
,
i.e., the constant map sending every element of 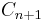 to the group identity in
to the group identity in 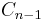 . This means
. This means 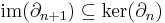 .
.
Now since each 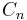 is abelian all its subgroups are normal and because
is abelian all its subgroups are normal and because 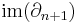 and
and 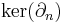 are both subgroups of
are both subgroups of 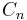 ,
, 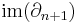 is a normal subgroup of
is a normal subgroup of 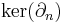 and one can consider the factor group
and one can consider the factor group
called the n-th homology group of X.
We also use the notation  and
and 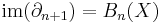 , so
, so
Computing these two groups is usually rather difficult since they are very large groups. On the other hand, we do have tools which make the task easier.
The simplicial homology groups 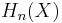 of a simplicial complex
of a simplicial complex  are defined using the simplicial chain complex
are defined using the simplicial chain complex 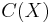 , with
, with 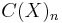 the free abelian group generated by the
the free abelian group generated by the  -simplices of
-simplices of  . The singular homology groups
. The singular homology groups 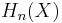 are defined for any topological space
are defined for any topological space  , and agree with the simplicial homology groups for a simplicial complex.
, and agree with the simplicial homology groups for a simplicial complex.
A chain complex is said to be exact if the image of the (n + 1)-th map is always equal to the kernel of the nth map. The homology groups of  therefore measure "how far" the chain complex associated to
therefore measure "how far" the chain complex associated to  is from being exact.
is from being exact.
Cohomology groups are formally similar: one starts with a cochain complex, which is the same as a chain complex but whose arrows, now denoted 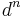 point in the direction of increasing n rather than decreasing n; then the groups
point in the direction of increasing n rather than decreasing n; then the groups  and
and 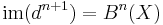 follow from the same description and
follow from the same description and
as before.
Examples
The motivating example comes from algebraic topology: the simplicial homology of a simplicial complex  . Here
. Here 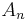 is the free abelian group or module whose generators are the n-dimensional oriented simplexes of
is the free abelian group or module whose generators are the n-dimensional oriented simplexes of  . The mappings are called the boundary mappings and send the simplex with vertices
. The mappings are called the boundary mappings and send the simplex with vertices
to the sum
(which is considered 0 if n = 0).
If we take the modules to be over a field, then the dimension of the n-th homology of  turns out to be the number of "holes" in
turns out to be the number of "holes" in  at dimension n.
at dimension n.
Using this example as a model, one can define a singular homology for any topological space  . We define a chain complex for
. We define a chain complex for  by taking
by taking 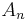 to be the free abelian group (or free module) whose generators are all continuous maps from n-dimensional simplices into
to be the free abelian group (or free module) whose generators are all continuous maps from n-dimensional simplices into  . The homomorphisms
. The homomorphisms 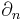 arise from the boundary maps of simplices.
arise from the boundary maps of simplices.
In abstract algebra, one uses homology to define derived functors, for example the Tor functors. Here one starts with some covariant additive functor  and some module
and some module  . The chain complex for
. The chain complex for  is defined as follows: first find a free module
is defined as follows: first find a free module 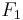 and a surjective homomorphism
and a surjective homomorphism 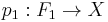 . Then one finds a free module
. Then one finds a free module 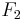 and a surjective homomorphism
and a surjective homomorphism 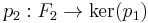 . Continuing in this fashion, a sequence of free modules
. Continuing in this fashion, a sequence of free modules 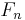 and homomorphisms
and homomorphisms 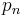 can be defined. By applying the functor
can be defined. By applying the functor  to this sequence, one obtains a chain complex; the homology
to this sequence, one obtains a chain complex; the homology 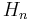 of this complex depends only on
of this complex depends only on  and
and  and is, by definition, the n-th derived functor of
and is, by definition, the n-th derived functor of  , applied to
, applied to  .
.
Homology functors
Chain complexes form a category: A morphism from the chain complex 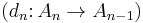 to the chain complex
to the chain complex 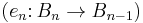 is a sequence of homomorphisms
is a sequence of homomorphisms 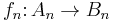 such that
such that 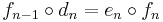 for all n. The n-th homology Hn can be viewed as a covariant functor from the category of chain complexes to the category of abelian groups (or modules).
for all n. The n-th homology Hn can be viewed as a covariant functor from the category of chain complexes to the category of abelian groups (or modules).
If the chain complex depends on the object X in a covariant manner (meaning that any morphism X → Y induces a morphism from the chain complex of X to the chain complex of Y), then the Hn are covariant functors from the category that X belongs to into the category of abelian groups (or modules).
The only difference between homology and cohomology is that in cohomology the chain complexes depend in a contravariant manner on X, and that therefore the homology groups (which are called cohomology groups in this context and denoted by Hn) form contravariant functors from the category that X belongs to into the category of abelian groups or modules.
Properties
If 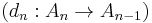 is a chain complex such that all but finitely many
is a chain complex such that all but finitely many 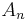 are zero, and the others are finitely generated abelian groups (or finite dimensional vector spaces), then we can define the Euler characteristic
are zero, and the others are finitely generated abelian groups (or finite dimensional vector spaces), then we can define the Euler characteristic
(using the rank in the case of abelian groups and the Hamel dimension in the case of vector spaces). It turns out that the Euler characteristic can also be computed on the level of homology:
and, especially in algebraic topology, this provides two ways to compute the important invariant  for the object
for the object  which gave rise to the chain complex.
which gave rise to the chain complex.
Every short exact sequence
of chain complexes gives rise to a long exact sequence of homology groups
All maps in this long exact sequence are induced by the maps between the chain complexes, except for the maps 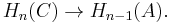 The latter are called connecting homomorphisms and are provided by the snake lemma.
The latter are called connecting homomorphisms and are provided by the snake lemma.
History
Homology classes were first defined rigorously by Henri Poincaré in his seminal paper "Analysis situs", J. Ecole polytech. (2) 1. 1–121 (1895).
The homology group was further developed by Emmy Noether[1][2] and, independently, by Leopold Vietoris and Walther Mayer, in the period 1925–28.[3] Prior to this, topological classes in combinatorial topology were not formally considered as abelian groups. The spread of homology groups marked the change of terminology and viewpoint from "combinatorial topology" to "algebraic topology".[4]
See also
- Simplicial homology
- Singular homology
- Cellular homology
- Homology theory
- Homological algebra
- Cohomology
Notes
- ^ Hilton 1988, p. 284
- ^ For example L'émergence de la notion de groupe d'homologie, Nicolas Basbois (PDF), in French, note 41, explicitly names Noether as inventing the homology group.
- ^ Hirzebruch, Friedrich, "Emmy Noether and Topology" in Teicher 1999, pp. 61–63.
- ^ Bourbaki and Algebraic Topology by John McCleary (PDF) gives documentation (translated into English from French originals).
References
- Cartan, Henri Paul and Eilenberg, Samuel (1956) Homological Algebra Princeton University Press, Princeton, NJ, OCLC 529171
- Eilenberg, Samuel and Moore, J. C. (1965) Foundations of relative homological algebra (Memoirs of the American Mathematical Society number 55) American Mathematical Society, Providence, R.I., OCLC 1361982
- Hatcher, A., (2002) Algebraic Topology Cambridge University Press, ISBN 0-521-79540-0. Detailed discussion of homology theories for simplicial complexes and manifolds, singular homology, etc.
- Hilton, Peter (1988), "A Brief, Subjective History of Homology and Homotopy Theory in This Century", Mathematics Magazine (Mathematical Association of America) 60 (5): 282–291, JSTOR 2689545
- Teicher, M. (ed.) (1999), The Heritage of Emmy Noether, Israel Mathematical Conference Proceedings, Bar-Ilan University/American Mathematical Society/Oxford University Press, ISBN 978-0198510451, OCLC 223099225
- Homology (Topological space) on PlanetMath
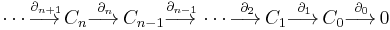
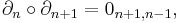
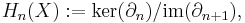
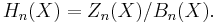
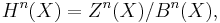
![(a[0], a[1], \dots, a[n]) \,](/2012-wikipedia_en_all_nopic_01_2012/I/1a16308d3fc63311eb449eb2f73ad1b6.png)
![\sum_{i=0}^n (-1)^i(a[0], \dots, a[i-1], a[i%2B1], \dots, a[n])](/2012-wikipedia_en_all_nopic_01_2012/I/53b3cf6cc1700065739bc9cd803dee21.png)